I wanted to get an order of magnitude sense of the utility of non-medical masks. Specifically their usefulness against floating droplets at a reasonable distance, and not from someone coughing loudly; those people can easily be avoided. In addition I focus on short term exposure. In other words, should I worry when waiting in an orderly line to order my take out frappuccino?
A note on methodology: I’m not cherry-picking data, but I am Google-picking papers, i.e. throwing terms in a search engine and using the first paper that has a chart that measured the thing I’m interested in. Comments are welcome if you find papers with orders of magnitude different results.
I look for worst case numbers, in terms of infection risk, because there’s a huge asymmetry in outcomes. If I overestimate the risk, the price is very low: I wore a mask for no good reason. If I underestimate the risk, the minimum price is to get infected, having my brains sucked out by a needle, followed by 10 days mandatory isolation with unpleasant symptoms. The maximum price is death and killing a whole bunch of others by accident. This difference is so massive that even a favourable result would not change my mask wearing behaviour, though it might make me feel better.
The first question is how many virus particles do you need to get infected? From watching This Week in Virology the magic number appears to be 250 (more than 100, less than 1,000). They cite a mouse study for this, but if I recall correctly also mentioned anecdotal evidence for humans.

Note that PFU means plaque-forming unit, which isn’t the same as a single virus particle / virion. So this math gets sloppy real quick.
Next we need to know how many particles the customer in front of you is breathing out, and how many of those stay afloat long and far enough to worry about.
Let’s assume this patient is maximally infectious, as people tend to be right before they develop symptoms and hopefully self isolate. According to this NIH infographic the maximum is 10^11 RNAs/mL. Since that may be an overestimate of infectious virions, so lets make it 10 billion.
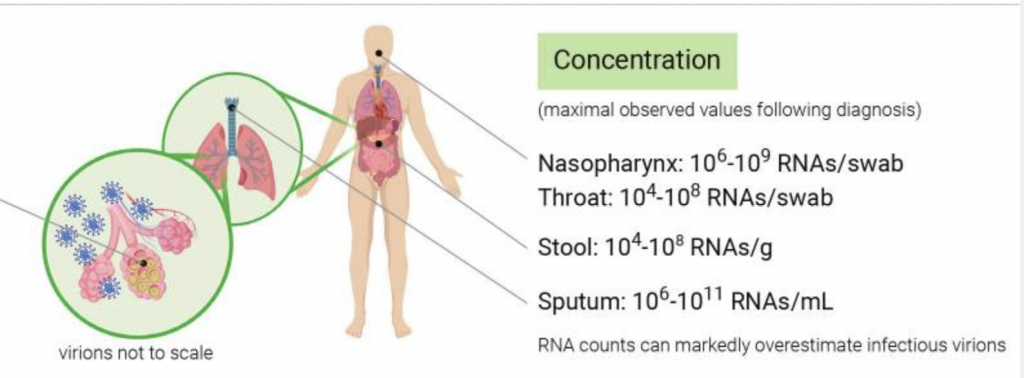
How many milliliters of sputum is this person blasting into the air in the course of the ten minutes they’re inside? And how much of that is likely to get anywhere near me?
Let’s also assume they’re talkative and obnoxiously loud. A 2019 study found that such people toss out up to 50 droplets per cm3 every 20 seconds. Let’s say an average of 10 droplets per cubic centimeter continuously.
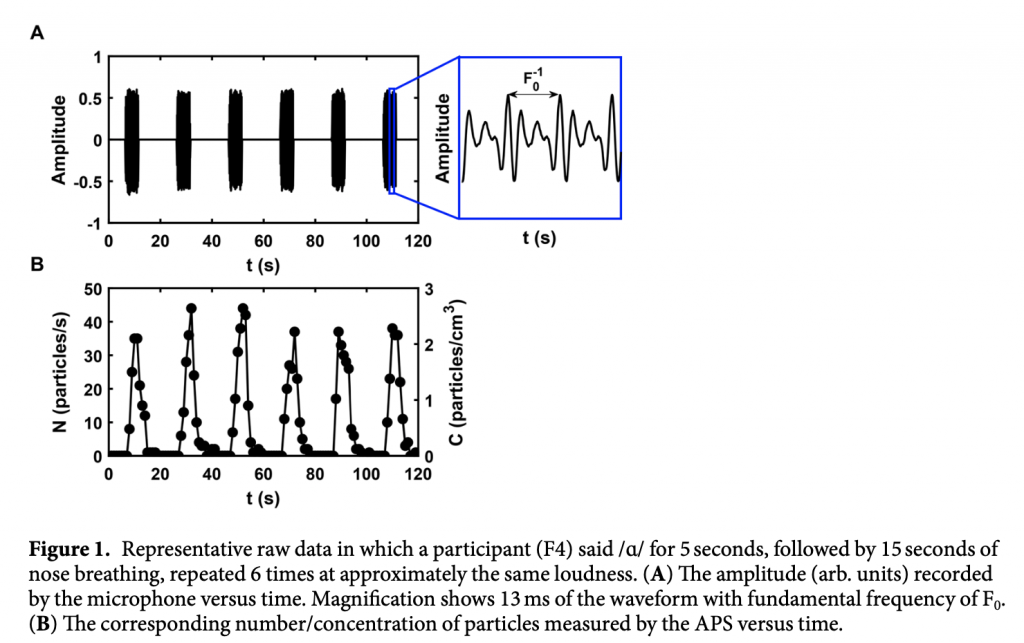
How many milliliters is that? Figure 2B from the same paper can help to guesstimate that. It shows the size distribution of the particles and we can derive volume from size.
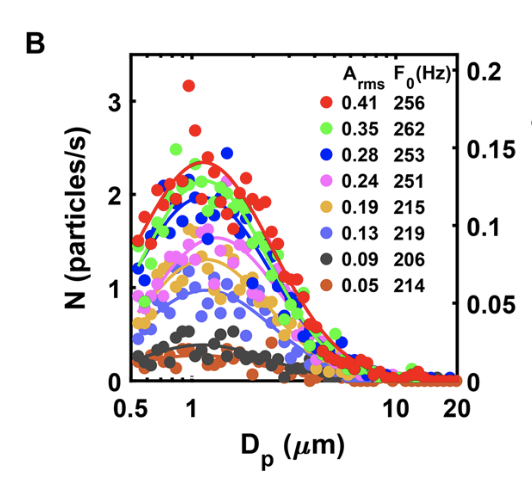
We only care about droplets that can reach us over some distance. Does the above chart suggest a cut-off size above which we can safely ignore droplets? A recent theoretical study says the following:
Our numerical calculations confirmed the effect of relative humidity on the number of suspended aerosols. At lower relative humidity, the maximum size of droplets that can fall 2 m away before evaporation is larger, which means more droplets could suspend in the air.
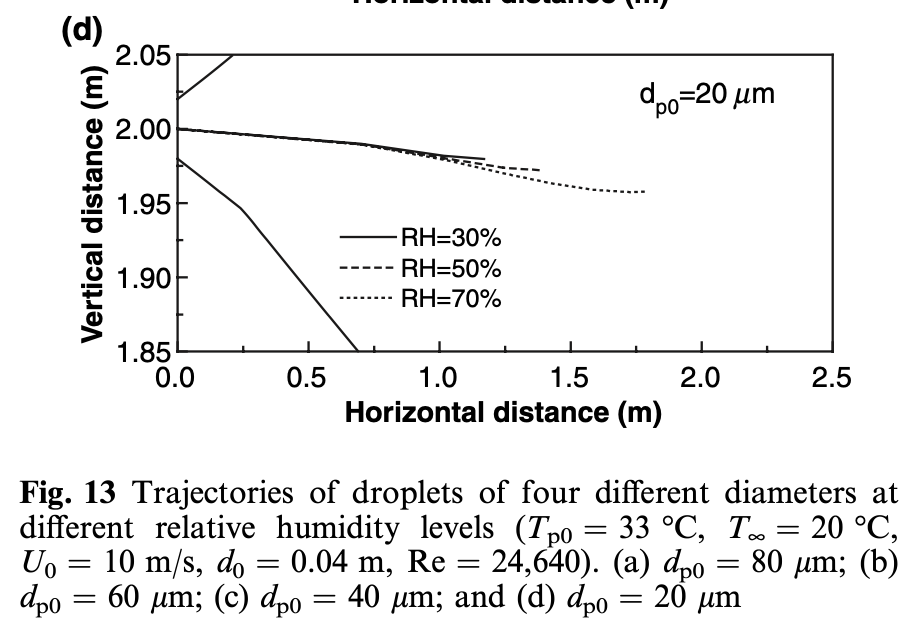
Let’s combine the above two charts. There’s a distribution of droplets from speech that are mostly smaller than 20 micrometers, and it seems these all evaporate into aerosols before they drop to the floor.
If we then assume each droplet has a diameter of 5 micrometers, i.e. a volume of 10^-10 milliliter, then our 10 billion PFU per mL means we can snugly fit one virus particle per droplet.
We exhale 5 liters of air per minute, so our patient exhales 50 liters during their 10 minute visit. That’s 50 droplets * 50,000 cm3 = 2,5 million virus particles floating in a cloud near you.
If this cloud spreads evenly over 10 cubic meters and you breathe in 50 liters (0.5% of that volume), you’re now the proud owner of 12,000 virus particles. Well above the 250 particle threshold we found at the top. In other words, you’re toast.
If your mask stops 90% you’re down to 1,200. If the patient wears a mask and it also stops 90% you’re down to 120 and get to survive. It gets better if the patient is less infectious, less talkative, the room is better ventilated, etc.

The above calculation could easily be off by two orders of magnitude in either direction, and perhaps masks are less efficient. But it does suggest that the one or two orders of magnitude protection offered by universal mask wearing can make the difference.
That’s just from a personal risk perspective. From a collective risk perspective, if a mask causes you to infect 20% fewer non-mask wearing people, and if others who wear mask reduce their own infection risk by 20%, that can take R=1.4 down to R=0.9. A 20% risk reduction on each side doesn’t seem unreasonable given the above numbers. Or the picture for that matter, or if you prefer video:
As the caveat section at the end of the video explains, it’s important to understand the difference between mask effectiveness (how often it prevents infection) from what percentage of particles it filters (for which I picked 90% in the above math). This effectiveness depends on a lot of things, not just how good the mask is, but also on how many particles are in the air. A very bad mask can still make a difference if it stops just enough virus particles from entering you, but it won’t help you when intubating a patient.
Before you think 90% is a ridiculous number, keep in mind that a N95 masks guarantees 95% reduction. Just like you can often eat food well beyond its expiration date, your non-rated amateur mask doesn’t have to be bad. Of course you’re free to pick a different number.
Finally, don’t forget to wear glasses.
More interesting mask math: https://youtu.be/Y47t9qLc9I4